Symbols for Dimensions and Planes

Symbols for Dimensions and Planes
Submitted by Peggy Hackney - April 22, 2005

Following are two papers concerning symbols for Dimensions and Planes developed by Carl Wolz in December 1983.

First is a paper by Carl that I presented for him at the 1984 LIMS Conference at Rutgers. In our Certificate Programs in Seattle, Berkeley and Utah our Integrated Movement Studies team has been using them since 1984, and have found them to be VERY useful. They do not, of course, deal with planes that are not in the cardinal dimensions.

Second is a tiny handout that we give our students that also deals with the issue of emphasis in the planes, and also that the symbols themselves do not enlarge to show timing. They are used with a duration line, linked with a continuity bow. They can also just be used by themselves in a Theme Bow.

Since these symbols have worked for us for over 20 years, I submit that they really solve the problem of how to indicate Dimensions and Planes without using the V, S, H in a square as is done at LIMS. I feel that we should get away from using English words as a basis for symbols whenever possible.

---

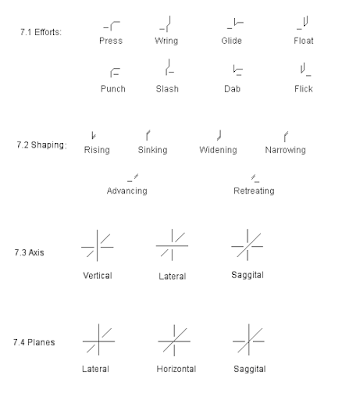
A Proposal for Symbols for the Three Primary Axes and the Three Primary Planes
By Carl Wolz, December, 1983

1.0 Various people working in Labanalysis have discussed the problem of no appropriate symbols to identify the three primary axes and the three primary planes of the body. This paper proposes a set of symbols for consideration.

2.0 The symbols are based on the convention of writing the three primary axes on a two-dimensional surface as follows:

3.0 The method for writing an axis would be to draw the axis being identified with a solid line and draw the other two axes with dotted lines. The symbols can be drawn within one square of graph paper; however, the dotted lines become difficult to read. Therefore, it is recommended that only one dash be drawn on each end of the lines being dotted.

4.0 The method for writing a plane would be to draw the two axes which define the plane with solid lines and draw the third axis--which is the line around which the plane revolves--with a dotted line. These symbols, similar to those for the axes, can be drawn within one square of graph paper with only one dash at the end of each line to represent dotted lines.

5.0 A theoretical problem with this method is that it does not reflect the directions of the corners of the planes; i.e. the points on the icosohedron. However, knowing the two axes of a plane make it simple to generate the corners.

6.0 It would be possible to use symbols for planes based on dotted lines in 5.1, 2, 3; however, these are not recommended for two reasons:

6.1 They do not fit easily into one square of graph paper.

6.2 They could get confused with rotation symbols or area signs.

7.0 A further argument for this proposal is that the symbols use elements similar to those used for Effort-Shape notation; i.e., horizontal, vertical, and diagonal lines, some solid, some partial. Effort-Shape symbols and Axis-Plane symbols are written below for comparison.

8.0 Summary

8.1 Symbols are based on the convention of draswing the primary axes of the body
on a two-dimensional surface.

8.2 Axes would be drawn with one solid line and two dotted lines.

8.3 Planes would be drawn with two solid lines and one dotted line.

8.4 All symbols can be drawn within one square of graph paper.

8.5 Symbols do not reflect the corner of the planes--the points on the icosohedron—
but rather show the two axes which generate the planes and the lines around which
the planes rotate.

8.6 These symbols use elements similar to the symbols for Effort-Shape notation.

9.0 The symbols for the axes and planes on graph paper:

Symbols for Dimensions and Planes (Developed by Carl Wolz in 1983)
By Peggy Hackney, June 2, 1996

 

Stress within the planes can also be recorded, which enables us to distinguish planes within various crystalline forms.


For instance, Ex. 2a indicates a vertical plane with emphasis in the up-down dimension (as is found in the Icosahedron). Ex. 2b indicates a vertical plane with emphasis in the side-side dimension (as is found in the Dodecahedron).

These symbols are drawn big for clarity in this posting, but they do not elongate. For instance, Ex. 2c says move in the horizontal plane for 4 counts.